2022年の仕事などの振り返り
いつの間にか2023年も1/3が終わりましたが
2022年の振り返りシリーズを完結できていなかったので
簡潔に書いて締めます。
2022年の仕事
1月~6月
2021年末から引続いて週1×3 +月1×1 で働いていました。
週1稼働の1社については
諸々の変化で自分の価値が全然出せなくなっていたことと
法人化準備の時間を確保するために契約を終了させてもらいました。
7月~12月
お金を得る仕事として週1×2 +月1×1で働いていました。
この期間で法人化し、個人事業主として契約していただいていたものも
全て法人での契約に切り替えてもらいました。
契約の主体が変わっても仕事の内容は変わらず、
データ加工のパイプラインの整備から
技術調査や営業管理の支援など多岐にわたり、
何でも屋おじさん(実際に対応できる範囲は狭いのですが)の道を突き進んでいます。
法人化しました②
前回に続いて法人化の諸々を記載します。
今回は調べたり考えたりしたことをQ&A形式でまとめました。
fqz7c3.hatenablog.jp
設立まで
・法人の形態はどうやって決めた?
最終的に合同会社を選択したわけですが、法人の形態は意外と多くて
私が理解しているものだけでも10種類近く存在します。
これらは大きく、非営利目的のものと営利目的のものに分けられます。
前者には一般社団法人や宗教法人などがあります。この中から選ぶと
税金面等のメリットがあるのではないかという邪な考えが一瞬浮かびましたが
営業活動を行う上で説明が面倒くさすぎるなと思って即却下しました。
後者の営利目的の法人(これが「会社」)には
株式会社、合同会社、合資会社、合名会社の4つがあります。
後ろ2つの合資会社と合名会社は会社が倒産した際の債務を
個人の財産からも弁済する義務を負う無限責任社員が必要になります。
無限責任社員は高いリスクに見合うだけのメリットがなさそうで、
かつ、法人設立数としても非常に少なかったのでこの2つも候補から外しました。
残った株式会社と合同会社ですが
これらの一番の違いは誰のお金で経営するかということだと認識しています。
株式会社の場合は
基本的には株主(経営者も株主である場合もある)の資金で経営するため、
経営に関して社外に対する説明責任が重く、色々な義務が課せられます。
一方の合同会社は基本的には社員(経営者)の資金で経営するため、
経営に関する説明責任はほとんどありません。
したがって、会社の運営負荷は完全に合同会社に分があります。
それに加えて、私はマイペースにやっていきたいという気持ちが強く、
他人の資本を入れないのが理想の姿だと考えているので合同会社を選びました。
今のところ、合同会社のデメリットは知名度の低さぐらいかなと思っています。
「合同会社ってことは誰かと一緒にやっているの?」と、たまに質問されます。
・本店所在地はどうやって決めた?
私は不動産を所有していないため、選択肢としては
借りるか実家の2択でしたが、旨味が大きいと考えた実家にしました。
・借りる
こちらは部屋を占有できる物理オフィスから
住所だけを使わせてもらうヴァーチャルオフィスまで幅があります。
ざっと調べた感じ、東京近郊の物理オフィスであれば10万円~/月ぐらいで
ヴァーチャルオフィスであれば1000円~/月ぐらいな相場でした。
物理オフィスは憧れもありましたが、通勤したくないですし
費用もかなり高かったので選択肢からはすぐに消えました。
ヴァーチャルオフィスは費用的には問題ありませんでしたが、
当たり外れが大きそうでかつ、もしサービスが終了した場合に
強制的に引越しや関連する手続きが発生する点が微妙だなと感じました。
・実家
実家はヴァーチャルオフィスの様な心配はほとんどありません。
しかし、現在住んでいる東京から物理的に離れており、
郵便物の受取と転送が必須でした。これについては
引退して暇そうにしている父に業務委託することで解消できました。
父に支払う費用はヴァーチャルオフィスに比べて割高ではありますが
以下の狙いもあり許容できると判断しました。
・父に仕事をしてもらうことで心身の健康を保ってもらいたい。
・両親共に歳を取ってきたので会う頻度を増やしたい。
・実家の片付けを計画的に進めておきたい。
・生まれ育った街がどんどん変わっていって帰省する度に寂しさを感じるので
もう少し街の変化を自分の身で感じたい。
・法人名はどうやって決めた?
個人事業主時代の屋号の反省も踏まえて私が考えた要件は以下でした。
・やりたいことが伝わる
・長くない
・ユニークで検索しやすい
・数年経っても飽きなさそう
表記は漢字、ひらがな、カタカナ、アルファベットから選ぶことになります。
漢字はやりたいことを伝えようとして連ねると中国語みたいになってしまい、
これを緩和しようと短くすると検索性が下がって難しそうだったので止めました。
ひらがなは狙いすぎている印象があり、よほどハマるものが見つからない限りは
嫌だなと思っていたので積極的には考えませんでした。
カタカナは元が英語なら英語のままの方がかっこいいですし
元が英語でない言葉を作り出すつもりはなかったので却下しました。
したがって、アルファベットの名前にすることを念頭において考え始めました。
アルファベットの名前は1単語でシンプルなものも、
いくつかの単語から文字を拾って作るタイプのものも良いな~と思っていました。
また、いずれの場合でも並び順のメリットがありそうなので
できれば「A」から始まる名前にしたいな~と思っていました。
1か月ぐらいあれこれ考えましたが、最終的には「A」で始まるというのを捨てて
1単語のものを社名としました。
余談ですが、考えている期間に友人と飲む機会があり、
みんなに適当な名前をあーだこーだ言ってもらったのはとても面白かったです。
・商標はどうして出願しなかったの?
これは、出願しても取れない可能性が高いと判断したからです。
法人名は他社と全く同じでも本店の所在地が異なれば登記できますが、
他社が商標登録を行っていると法人名の使用に支障が出る場合があります。
そのため、本来は法人名の要件に入れて考えるべきでしたが
そこまで気が回っておらず印鑑を発注した後にこのことに気付きました。
慌てて調べてみると、国内の企業では登録はなかったのですが
綴りが1字違い(読みは同じ)のアメリカの企業が国際商標を取得していました。
見つけた瞬間に「うっわ」という声が出てしまいましたが、
現状はその企業の日本での事業展開は大規模ではなさそうだったので
当社が制限を受ける可能性は低いのではないかと考えました。
また、この国際商標があるために、同様の読みの商標を
国内の企業が取得できる可能性も低いだろうと考えて
法人名を考え直したり商標を出願したりする必要はないと判断しました。
・資本金の額はどうやって決めた?
資本金は少なすぎても多すぎてもデメリットがあります。
上限については、設立初年度に消費税の免税事業者になる要件に
資本金が1000万円未満というものがあるため、これを意識しました。
一方、下限については低くしても税金的なデメリットはありませんが
会社や経営者の信用という観点から
最低でも200万円ぐらいはあった方が良いのかなと考えています。
200万円の根拠はあまりないですが
月に10万円ずつ出ていっても少なくとも1年間は保つというぐらいの感覚です。
私の場合は見栄を張って、この下限から少し余裕を持たせた額で決めました。
・決算月はどうやって決めた?
決算月は設立月とは関係なく決めることができます。
これは1期目の営業期間を決定できるということでもありますが
短くするメリットはほとんどないと思いましたので
設立から丸1年となるように設定しました。
ちなみに、3月決算の場合は税理士さんも忙しくて対応してもらいにくかったり
決算月が上半期だと相対的に税務調査に入られやすいという噂があったりしますが
決算月を左右する積極的な理由にはならないように思いました。
設立以降
・社宅料はどうやって決めた?
社宅賃料の全額を法人が払うと個人としては都合が良い様に思えますが
そうすると、現物給与の支給とみなされて
税金が掛かったり社会保険料が上がったりします。
これを回避するために、個人は現物給与に相当する金額以上を
社宅料として払う必要があります。
また、面倒なことにこの金額は所得税と社会保険料で異なります。
所得税はこちらから、社会保険料はこちらから算出されますが、
一般的には社会保険料の方が高くなることが多いのではないかと思います。
私の場合は所得税と社会保険料の差は数千円程度でしたので、
所得税としては現物給与とみなされないが社会保険料としては
一部現物給与とみなされるラインの社宅料にしました。
・役員報酬をいつから払うかどうやって決めた?
1か月目から支払う場合は以下の負担が発生するので
2か月目以降に支払いを開始することに決めていました。
・源泉所得税の納付
納期の特例承認を受けていても
1か月目の分は適用外となるため翌月に所得税を納付する作業が必要になる。
・社会保険等の加入手続き
役員報酬の支払いを開始してしまうと加入手続きを進める義務が発生する。
逆に期限としては、役員報酬は3か月以内に支払いを開始すれば
損金として認められるルールになっていますが
役員賞与の届出は設立から2か月以内に行うことになっており、
また、2か月目には設立当初に比べてだいぶ余裕ができていたこともあって
2か月目から役員報酬の支払いを開始することにしました。
・役員報酬と役員賞与の金額はどうやって決めた?
キャッシュフローの管理で頭を悩ますことは避けたかったので
毎月の役員報酬は社会保険に加入できる程度にして
決算月にまとめて役員賞与を支払うことにしました。
役員賞与額の決定は悩ましいところですが
法人として稼いだお金は所得税率が一定となるように
毎年コンスタントに個人に移転するのがベストな戦略であると考えているので
初年度赤字になっても良いという覚悟で強気の設定にしました。
ちなみに裏技な感じですが、役員報酬を下げて役員賞与でまとめて支払うと
社会保険料のテーブルの上限に達して社会保険料率を下げることができます。
当然、払い込む厚生年金が減るので将来貰える額は減りますし
あまり露骨にやると年金事務所から怒られるらしいので塩梅には注意が必要です。
・初年度赤字になってもデメリットはないの?
現状、銀行から融資を受ける予定はなく、デメリットはないと考えています。
・企業型確定拠出年金は考えなかった?
いくつかの金融機関のプランを見ましたが
どこも社員数に依存しない固定の手数料が年に10万円程度かかる様だったので
お得感はないと判断して止めました。
もし社員数が5人以上になったら考えるかもしれません。
・税理士と契約しなくても大丈夫?
今のところは問題ありません。
freee会計の入力で悩むことが時々ありますが
チャットで問い合わせて解決してもらえることがほとんどです。
確定申告については、1年目はfreee申告を契約しようと考えており、
大した内容でなければ2年目以降は自力で行うつもりです。
・IT導入補助金はどうして使わなかったの?
freee会計は契約する予定だったので、補助金が利用できないか探ってみましたが
割高なプランしか対象にしてもらえませんでした。
そのため、お得感は全くなく、手続きも大変そうだったので止めました。
・個人事業主はどうしてオーバーラップしてたの?
個人事業主として締結済みの契約を法人に引継ぐには
契約の変更手続きなどが必要になります。
これはお客さんの負担にもなるため契約の引継ぎは行わないことにしました。
そのため、役務の提供期間としては個人と法人とで重ならないように注意して
個人の売掛金が解消するまでの期間について個人と法人とが共存していました。
・個人事業主として普通徴収されていた個人住民税の手続きって何か必要?
必要ありません。毎年市区町村への提出が義務付けられている
給与支払報告書に基づいて普通徴収から特別徴収に切り替えられるそうです。
・郵便物の転送頻度はどのくらい?
月に0回~2回です。設立から数か月経って0回の月も増えてきました。
郵便物が届いたら写真を送ってもらうようにしていて、
必要であれば開封もしてくれるので、現物を受け取る必要がほとんどありません。
また、現物が必要なものでも、急ぐものは基本的にないので
いくらかまとまったタイミングで送ってもらっています。
法人化しました①
年末に公開するつもりで書き始めましたが
思いのほか長くなり、1月も終わるタイミングになってしまいました。
2022年の振り返りをこれから3回に分けて公開します。
2021年の記事に書いていた通り、個人事業主から合同会社へ法人成りしました。
今回の記事では設立に際して行ったことを中心に記載します。
私はもう合同会社を設立することはないと思いますが
これから合同会社を作ろうと思っている方に
先回りしてイメージを掴むのに役立てていただければという気持ちで書いています。
今回と次回の記載内容は、
2022年のある期間において役員1名だけの合同会社を設立した際の
ルールやシステム、キャンペーンなどに基づいて記載していますので
今後は諸々変更になっている可能性があることにはご注意ください。
全体感
士業の方々の力は借りず、全て自力で手続きを行いましたが
合同会社は株式会社に比べて負担が少ないこともあり、
想像していたよりは苦労しませんでした。
デジタル庁が提供している法人設立ワンストップサービスを利用することで
基本的にはオンラインで手続きができました。
こんなに便利な仕組みを作ってくれたデジタル庁には感謝です。
ちなみに、オンラインでできなかった手続き等も郵送で対応でき、
法務局や税務署、年金事務所等に出向く必要はありませんでした。
手続きや税金に関して分からなくて悩んだ点は
国税庁等の公式な文書を読み込むか、役所等に電話して解消していきました。
当初は会計ソフトや税理士事務所のブログなどを参考にしていましたが、
条件付きでしか正しくない説明や明らかに誤った見解などの記述が気になり
公式な情報に当たるのが早道だなと思うようになりました。
ちなみに、役所等への問い合わせにはコツがあるなと感じました。
リテラシーが低い方からの問い合わせが多く、かつ、忙しいからと推測しますが
質問の意図をしっかり理解する前に
調べればすぐに分かる正常系の手続きの説明を始められることが多いです。
このステップを挟むのが面倒だったので、なるべく正常系の説明を自分で行って、
その上で自分のケースが適用できない可能性があることを指摘して
どう対応するのが正解なのか質問するようになりました。
行ったこと
設立日からの相対的な期間で記載します。
同じセクション内では分かりやすさを優先して
実際の順序から変更している箇所があります。
2か月前
・創業手帳の入手
法人化のことを調べ始めるまで存在すら知らなかったのですが
創業手帳は法人設立に関するフリーペーパーです。
法人設立の前後で関わる企業の広告が多くて読むべきところは少ないのですが
「創業前後のスケジュール」と「税金イベント一覧」が役に立ちました。
法人設立ワンストップサービスの存在もこの雑誌を見て知りました。
・会社の形態の決定
あまり悩まず合同会社とすることにしました。
詳細については次回の記事に書きます。
・加入する健康保険組合の決定
何も考えなければ協会けんぽ一択なのですが、
条件によっては加入できる健康保険組合もあるはずなので探してみました。
協会けんぽより保険料率が低く、業種的にも入れそうな組合もあったのですが
事業所の社会保険加入期間や被保険者数などの条件が厳しいところばかりで
設立してすぐに入れそうなところは見つけられず、
素直に協会けんぽに入ることにしました。
・登記に利用する住所の決定
こちらは少し悩みましたが、実家の住所で登記することにしました。
詳細については次回の記事に書きます。
・法人名(商号)の決定
法人名を決定しないと印鑑を発注できないので
クリティカルパスであることを意識した最初のタスクでした。
1か月ぐらい考えて、最終的にアルファベットの名前に決定しました。
詳細については次回の記事に書きます。
4週間前~
・経営セーフティ共済の減額
個人事業主として節税目的で加入していましたが
2022年は個人事業主の期間が数か月間しかなく、
大した所得にならないことに気付いて減額の手続きを行いました。
後に判明するのですが、個人から法人に契約を承継するタイミングでは
金額の変更ができないので、変更するなら法人化の前に行うのが正解です。
・印鑑の発注
自分で印鑑を買うのは初めてだったので色々調べました。
材質の違いや同じ材質でも買うところによって値段がピンキリで悩みましたが
最終的に、評判が良かったハンコヤドットコムの法人設立セットに決めました。
後述しますが評判通り良かったと思っています。
・登記の添付書類の作成開始
定款含めて諸々の作成を開始しました。
当初は、法人設立手続きをfreee会社設立で行うつもりだったので、
こちらに情報を入力して標準的な定款を作成しました。
ここで作成した定款をダウンロードし、細かい修正を行って完成させました。
定款の事業目的については書き方にクセがあるので、
同業他社や以下の様なサイトの記載を参考にして書きました。
・就業規則等の作成開始
従業員を10人以上雇用しない場合は就業規則等の作成は必須ではないのですが
節税の観点から社宅利用規定と出張旅費規程を作る必要があり、
これらの規程の親となる就業規則もある方が自然なので作成することにしました。
厚労省からモデル就業規則が公開されているので、こちらをベースにしました。
厚労省が公開しているものなので、当然ながら
従業員が不当な扱いを受けないことを重視して作られています。
これ自体は悪いことではないですが、不当な扱いさえ受けなければ
働きやすいかと言えばそうでもないだろうという印象でしたので、
各種法律等を参照しながらゆるめる部分はゆるめて
厳しくする部分は厳しくして完成させました。
自分の会社がどうありたいかを考えながら
ルールを作成するというのはなかなか面白かったです。
従業員を雇う予定は当面ないのですけれど。
・賃貸物件の名義変更手続きの書類の入手
自分が住んでいる賃貸物件を法人の社宅とすることで節税ができます。
法人名義の契約とする旨について賃貸の管理会社に連絡して
手続きに必要な書類を予め送ってもらいました。
・iDeCo(個人型確定拠出年金)の手続きの書類の入手
厚生年金に入って第1号被保険者から第2号被保険者に変わると
iDeCoの拠出限度額が変更されます。
この変更を申請するための書類を証券会社から予め送ってもらいました。
2週間前~
・印影の校了
おそらく、社名にアルファベットが入っているとデザインが難しく、
1回目に送られてきたデザインはかなり微妙でした。
ただ、社名の意図やどのような印象を望むかなどをお伝えしたところ
格段に良くなり、かつ、納得いくまで修正してもらえた(計4往復)ので
最終的にはとても満足できるものになりました。
注文する時点ではあまり気にしていなかったのですが、
丁寧に校正に付き合ってくれるところに発注できて良かったと思いました。
・備品等の売買契約書の作成
個人事業主として使用していた備品や
法人として使用するために先行して購入した備品等を
法人の物とするための売買契約書を作成しました。
・オンラインストレージの決定
総社員の同意書や就業規則などの存在を
タイムスタンプ付きで証明できる仕組みが必要と考えて
オンラインストレージを探し始めました。
ほとんどの企業がミニマムのプランでも月数千円かかる感じで
イメージしていた価格帯と合わないな~と思っていたところ、
セキュアSAMBAのフリープラン(5GB)だと無料で使えるということが分かり
こちらを使うことにしました。
・名刺のデザイン作成
前回利用したデザイン名刺も特に不満はなかったのですが、
時間の余裕があったこともあり、
サイト上でデザインを作成できるラクスルで作ってみました。
パワーポイントとほぼ同じ感じで操作でき、
あまり悩むところもなく良かったです。
ただ、プレビュー時の裁断で切り落とされる可能性がある幅がかなり太くて
これをどう考えるべきかは悩みました。
1週間前~
・印鑑の受取
デザインについては確認済でしたが、改めて実物を見て満足しました。
・登記の添付書類の完成
定款等の記載を全て完成させました。
・登記の添付書類の電子署名付与
法人設立ワンストップサービスで登記の申請を行う場合は
提出する各ファイルに電子署名が必要です。
電子署名を行う方法はいくつかあるようですが
今回初めてで分からないことだらけだったので、情報を見つけやすかった
マイナンバーカードとPDF署名プラグインを使う方法で行いました。
これには有償のAdobe Acrobatが必要なのですが
7日間のフリートライアル期間もしくは
課金が始まって14日以内に解約すれば実質無料で利用できます。
ちなみに、Adobe Acrobatが必要だったのはこの1日だけでした。
さらに蛇足で、普通にAcrobatをインストールすると64bit版が入るのですが
PDF署名プラグインが32bit版にしか対応していないという落とし穴があります。
32bit版をインストールするためにサポートに問い合わせたり地味に苦労しました。
今後はこの辺り改善されると良いなと思います。
・資本金の振込
資本金があることの証として自分の銀行口座に振り込みました。
発起人が複数人いる場合は入金した人の氏名が必要なので振込が必要ですが
1人の場合は誰かは自明ですので入金でもOKだそうです。
この振込のタイミングは登記の2週間前以降でかつ、
定款作成日以降である必要があります。
・法人設立ワンストップサービスの申請情報の作成開始
法人設立ワンストップサービスから申請するものは登記だけでなく、
税務署や都道府県や市町村に申請するものもあり膨大です。
申請情報入力は事前に行うことができるので、2日前から入力を開始しました。
申請項目は一覧を上から全て見て、それぞれ「要」か「不要」か判断しました。
微妙に内容が異なるなど紛らわしいものがあるので注意が必要です。
法人設立日
・会社のウェブサイトのレンタルサーバーの申し込み
レンタルサーバーを使うのは初めてでしたが、色々検討して
ロリポップのハイスピードプランにしようと事前に決めており、
日付をまたいだタイミングで申し込みを行いました。
このタイミングでドメインも取得する想定だったのですが
ドメインずっと無料のキャンペーンを適用するためには
法人の場合は1週間待たないといけないという縛りがあり、
狙っていたドメインが取れるかもう1週間ドキドキすることになりました。
こんな大事なことが書かれていなかったこと以外には
今のところ特にストレスなく利用できています。
・法人設立ワンストップサービスの申請
2日前から作成していたものを完成させて午前中に申請しました。
おそらく、入力に合計で3時間近くかかりました。大変でした。
・登録免許税の電子納付
申請するとすぐに登録免許税(6万円)の電子納付の情報が出てくるので
資本金を入金した口座から納付しました。
この後は登記完了の連絡が来るまで待ちかなと思っていたら
3時間後ぐらいに法務局から不備の指摘の電話がありました。
指摘内容は「定款の住所は市まででOKだが登記する住所は全て必要」という
軽微なものだったので法務局側で修正してもらえました。
・挨拶&契約更新の手続き開始
個人事業主として仕事をしているお客さんには
事前に法人設立のお知らせをしていましたが
改めて法人設立の挨拶と今後の契約を法人に切り替えてもらうお願いをしました。
・備品等の売買契約締結
事前に作成していた契約書に押印しました。
・会社ウェブサイトの作成開始
自分でウェブサイトを作成するのも、WordPressも初めてでしたが
BusinessPressというちょうどよい感じのテーマを見つけてからは
あまり苦労せずに作成を進めることができました。
また、サイト内で利用する写真については
商用利用可能でかつクレジット表記不要でカッコいい写真が多い
pixabayから探しました。
作成するのが一番大変だったコンテンツはプライバシーポリシーですが
こちらについてはお客さんや同業他社の記載を参考にしながらまとめました。
翌日~
・登記の完了
2営業日後に完了の連絡が来ました。
・登記事項証明書の申請
銀行口座の開設などに必要な登記事項証明書をオンラインで申請しました。
同時に印鑑証明書も申請したかったのですが、印鑑証明書の発行には
印鑑カードが必要ということをこのタイミングで知りました。
印鑑カードの申請は登記の完了を待つ必要もないので
登記と同時に進めておくのが正解だったようです。ちょっと失敗しました。
・印鑑カードの申請
慌てて印鑑カードの申請を郵送で行いました。
1週間後~
・ドメインの取得
ようやく1週間経ち、無事狙っていたドメインを取得することができました。
・会社ウェブサイトのドメイン設定
ロリポップのドメインから取得したドメインに切り替えました。
あまり調べずに雰囲気でやっていたら
WordPressの管理画面に入れなくなって焦ったので
初心者はちゃんと調べてからやった方が良いですね。
・メール等の設定
Gmailで送受信できるように設定しました。
・名刺の発注と受取
お客さんとの打ち合わせが決まったので
空欄にしていたドメイン部分を完成させて発注しました。
紙は高級紙というものを選択したのですが、
受け取った名刺の感じはちょっとイメージと違いました。
もし次回発注することがあれば別の紙にしようと思います。
プレビュー時に心配していた裁断ラインのブレは全く気になりませんでした。
・登記事項証明書の受取
申請してから1週間かからないぐらいで届きました。
2週間後~
・印鑑カードの受取
こちらも1週間ぐらいで届きました。
・印鑑証明書の申請
印鑑カードが来たので、印鑑証明書の申請をしました。
また、登記事項証明書も最初に申請した3枚では足りないことが
この時点で明らかになっていたので併せて申請しました。
登記事項申請書は様々なシーンで提出を求められ、かつ、返却してもらえないので
最初から5枚ぐらい発行してもらうのが良い気がしました。
印鑑証明書は登記事項証明書より1,2枚少なくていい感じだと思います。
・銀行口座の開設の申込み
個人事業主としての契約を法人へ切り替えるためにも銀行口座が必要です。
銀行は大きく、ネット銀行と、オフラインがメインの銀行に分けられます。
前者の方が審査もゆるく、口座開設までの期間が短い傾向があり、
後者の方が審査も厳しい分、信用度が高かったり、
後者でしかできない取引(経営セーフティ共済など)があったりします。
銀行口座は複数持っていて悪いことはないので、
GMOあおぞら、楽天、三菱UFJの3行で開設することにしました。
まずは、法人としての営業活動を証明する書類がなくても、
個人事業主としての契約書で対応してもらえる
GMOあおぞらネット銀行から開設手続きを始めました。
3週間後~
・賃貸物件の名義変更手続き
登記事項証明書を入手したので名義変更の手続きを進めました。
書類に現在の給料を記載する欄がありましたが、
この時点ではまだ役員報酬の支払いを開始していなかったので
役員賞与まで含めた想定の金額を備考欄に記載しました。
また、設立間もない法人で信用はゼロに等しいと認識していたので
連帯保証人(私個人)の信用を上げるために
確定申告書のコピーを添付して提出しました。
・備品等の売買契約の履行
個人事業主として使用していた備品等を全て法人の物とし、
法人宛に請求書を発行して個人の口座に代金を振り込みました。
個人事業主としては経費と相殺させるため売上として計上しました。
・SNSでの報告
昔の上司や同僚などからコメントやメッセージをいただけて嬉しかったです。
・freee会計の契約
個人事業主としてはマネーフォワードを利用していましたが
一方的なプランの変更やサポート品質の低さにブチ切れた見切りをつけており
freeeに乗り換えることに決めていました。
年払いのプランにするので事業最終年度の翌年に費用が発生しないように、
また、5000円のAmazonギフト券がもらえるキャンペーンが適用になるように
設立から4週間経ったタイミングで契約しました。
サポートはたまに怪しいことも言いますが
基本的には手厚く対応してもらえて現時点では好印象です。
・銀行口座(GMOあおぞらネット銀行)の開設
予想していたよりは時間がかかりましたが
これでお客さんに銀行口座をお伝えすることが可能となりました。
・法人としての契約締結
個人事業主として契約していた仕事を
翌月から法人としての契約に切り替えてもらうために契約手続きを行いました。
また、元々単価を低めで契約していたお客さんについては
少しだけ単価を上げてもらっています。
1か月後~
・賃貸物件の名義変更手続きの審査通過
無事通過しました。
・賃貸物件の固定資産評価額証明書の取得
所得税で現物給与とみなされない社宅料を計算するために必要な
固定資産評価証明書を都税事務所に発行してもらいに行きました。
本人確認書類と自分が賃貸の貸借人であることを証明するために
契約書を持参する必要があります。
・社宅料の決定
諸々を考慮して役員として毎月1万円を社宅料として払うことにしました。
また、この計算プロセスについて社宅利用規定に厳密には記載していなかったので
今回の算出ケースが適合するように追記および修正を行いました。
詳細については次回の記事に書きます。
・残りの銀行の開設の申込み
法人として仕事の契約も結べたので
楽天銀行と三菱UFJ銀行の手続きを開始しました。
GMOあおぞらネット銀行が開設できたので
同じネット銀行である楽天銀行は不要かも?と思ったのですが
念のため開設しておくことにしました。
後から分かったのですが、GMOあおぞらネット銀行はPay-easyが使えず
社会保険料の納付ができなかったので楽天銀行も開設して正解でした。
・三菱UFJ銀行のオンライン面談
少し身構えていましたが、個人事業主からの法人成りであることや
事業内容等について10分程度やりとりをしたら終了しました。
正直、何をチェックされているのか全く分かりませんでした。
・信用調査会社のインタビューのお断り
聞いたことのない会社から会社情報のインタビューの申込みの電話がありました。
クライアントから依頼を受けて調査を行っているとのことで
どちらかの銀行だろうと思いましたが、どこかは教えてもらえませんでした。
銀行であれば、インタビューを受けないことで審査に落ちたとしても
クリティカルではないなと考えてお断りしました。
もし断るデメリットがあったとしても、
開示した情報の取り扱いについての契約が何もない状態では
リスクが高過ぎるなと感じたので受けなかった可能性が高いです。
・役員報酬と役員賞与の金額の決定
毎月の役員報酬は社会保険に加入できる程度にして
決算月にまとめて役員賞与を支払うことにしました。
大事なことなので、総社員の同意書を残しました。
詳細については次回の記事に書きます。
・事前確定届出給与の申請
役員報酬や役員賞与の金額を期中に自由に変更できるのであれば
法人税を簡単に減らすことができてしまいます。これを封じるために
事前申請されたものしか経費にできないというルールがあります。
そのため、申請を法人設立ワンストップサービスから行いました。
・社会保険の加入手続き
年金事務所の説明でも提出時期は「事実発生から5日以内」と記載があり
設立してすぐに対応しないといけない印象を受けますが
設立の当月から役員報酬を支給するのでなければ
届け出ても手続きを進めてもらえません(と明記しておいて欲しい)。
この月から役員報酬を支給するのでようやく手続きができるようになりました。
この手続きは法人としての加入手続き(新規適用届)と
社員を登録する手続き(被保険者資格取得届)、
社員の扶養家族を登録する手続き(被扶養者届)があります。
私は扶養している家族はいないので上記2つが必要な手続きでした。
単一のシステムで対応できると便利だったのですが
法人設立ワンストップサービスは新規適用届しか対応していなかったので
一旦こちらから新規適用届を申請して、
後追いで被保険者資格取得届をe-Govから申請しました。
・社会保険の再申請
申請の数日後に新規適用届の申請が却下されました。
電話で問い合わせてみるとe-Govのデータ連携関連の障害が起きており、
被保険者資格取得届が年金事務所に届いていなかったことが分かりました。
何週間も前から起きている障害情報を周知させない運用に憤りつつも
すぐには解決しそうにないことを理解したので、
被保険者資格取得届のキャプチャ画像を添付して新規適用届を再申請し、
被保険者資格取得届の原本は郵送することで対応しました。
・給与支払いフォーマットの作成
特に定められたフォーマットはないので、
所得税や社会保険料の算出過程が分かる形で作成しました。
・扶養控除等申告書の作成
税務署から税金周りのマニュアルや用紙一式が郵送されてくるので
その中から扶養控除等申告書を探し出して作成します。
一応、最初の給料を貰うまでに事業主に対して提出するルールになっています。
・iDeCoの手続き
社会保険の加入手続きが済んでから書類を提出しましたが
時間がかかるため、もっと早く手続きを行っていた方が良かったみたいです。
また、後述のiDeCo+で会社が負担する分があるので
従業員負担の金額はこれを差し引いて提出する必要がある点に注意が必要でした。
私は会社負担分と合算して記載していたため1回差し戻されてしまいました。
・iDeCo+の事前申請
iDeCo+の申請を行うことで、iDeCoの拠出金額の一部(最大2.2万円)を
会社の経費として支払うことができるようになります。
公式の資料を読む限りだいぶ面倒そうな手続きだったので
まずは事業所番号を発行してもらうための手続きだけを行いました。
後の手続きに必要な書類は別日に地道に作成しました。
・銀行口座(楽天銀行)の開設
実家の固定電話に銀行からの留守電が何度か入っていたみたいですが
結局、誰も出てくれないままでしたが開設してもらえました。
・健康保険証の受取
再申請から2週間ぐらいで届きました。
忙しい時期だともう少し時間がかかるかもしれません。
2か月後~
・任意継続していた健康保険の脱退手続き
脱退手続きを郵送で行いました。前納していた保険料は
加入資格を失った翌日(協会けんぽに加入した日)以降の分が払い戻されます。
ちなみに、国民年金も前納していましたが
こちらは特に手続きをしなくても自動的に払い戻されました。
・銀行口座(三菱UFJ銀行)の開設
返送するべき書類の押印を失敗して用紙を再送してもらっていたこともあり
時間がかかりましたが、開設できました。
・国税ダイレクト納付の登録手続き
ダイレクト納付が可能な銀行口座が開設できたので郵送で手続きを行いました。
・個人事業主としての最後の入金
売掛金が0円になり賃借対照表も綺麗になったので
個人としての事業活動を完全に終了しました。
・事業廃止等申告書の提出(地方税)
個人事業税の対象とはなっていませんでしたが
廃止の申告を郵送で提出しました。
・廃業届、青色申告取りやめの提出(国税)
こちらはe-Taxから提出できました。
・中小企業庁の共済の手続き
小規模企業共済と経営セーフティ共済の手続きを銀行で行いました。
小規模企業共済は引き落としの口座は変わらず、
同一人通算の手続きを行うだけで良かったので簡単でした。
一方の経営セーフティ共済は引き落としの口座が個人のものから
法人のものに変わり、かつ、口座を開設した支店が異なるためかなり大変でした。
承継前後の口座の支店が異なる場合は、中小企業庁と金融機関の両方に対して
事前に手続きを確認しておくことをお勧めします。
また、金融機関の窓口の方も慣れていない場合が多く、
不正確な案内をされたことがあったので、丸腰で臨むのは避けた方が安心です。
・iDeCo+の登録通知の受取
提出から3週間後ぐらいに受け取りました。
予想していたより時間がかかりました。
・iDeCo+の本申請
拠出を開始する前月の20日が締切でしたので慌てて
予め作成しておいた書類群の事業所番号を埋めて本申請を行いました。
・eLTAXの利用届の申請
PCdeskというシステムから申請を行いました。
次回は主に調べたり考えたりしたことを書きます。
独立後3年目の振り返りなど
今年は年末の振り返りが唯一の記事になってしまいました。
技術的に書けるネタも色々あったので来年は頑張って書こうと思います。
以下、独立して3年目の記録です。
今年の仕事
1月~2月
週3×1 + 週2×1 + 週1×1 +月1×1 という感じで4社の仕事を行っていました。
頭の切り替え負荷、非稼働日の活用度などの観点からギリギリだなと感じました。
週2→週3に増やした仕事については
プロジェクトへの関与度が上がることで
メンバーとの一体感が増して充実感がありました。
週2で新たに始まった仕事については
かなり活用しにくい形でデータが蓄積され始めていたので
データ周りの整備に徹する形となりました。
週2→月1に減らした仕事については
定例の打ち合わせなどは全てカットし、
必要な時に声を掛けてもらう感じにしました。
案件のちょっとした相談と、プロパーに任せるには効率が悪い
(手間もかかるし成功確率も高くない)PoCを中心に対応しました。
過去2年間週2で働いてきた蓄積もあり
月1でも十分に対価に見合う働き方はできるなと感じました。
3月~9月
一時的に増やしていた週3の仕事が週2に戻り
週2×2 + 週1×1 +月1×1 という感じで落ち着きました。
週2に戻った仕事は4月のタイミングで組織の変更があり
プロジェクトの立上げメンバーが異動になりました。
思いを持って仕事をされていたのに
サラリーマンという働き方は残酷だなあと思いました。
また、組織と方針の変更に伴い、新機能の開発よりも
既存のデータ品質の向上と、外部データのスムースな統合に
重点を置くようになり働き方もやや変わりました。
冬から始めた週2の仕事も
春には大きな落とし穴にはハマらずある程度信頼できる集計ができる状態になり
久しぶりに集計レポートを作成したりレビューに参加したりしました。
そこで、改めて集計レポートの作成でさえ簡単ではないと感じました。
数字が発生するメカニズムに思いを馳せなければ
容易にミスリードしたり、意図せず嘘をついたりしてしまいます。
また、結果の表現についてもフォーカスを絞らなければ
情報過多で読み手の負荷の高い資料が生まれます。
自分はこれまでの様々な経験を通して
ある程度の品質のアウトプットができるようになったと自負していますが
このスキルを他者へどう伝えるか
教育するかという意味で難しさを感じました。
週1の仕事については、関わっていた機能がリリースされ
ついに日の目を見ることになりました。
10月~12月
年初に働き過ぎて税率が高くなることが確定してしまったこともあり
週2の仕事を週1に減らしてもらい、週1×3 +月1×1 になりました。
ようやく時間ができたので読みたかった本を読んだり
コロナも収まっていたので神奈川へ日帰り旅行を何度かしたりしていました。
以下の本は読んで良かったと思いました。
テスト駆動開発 | Kent Beck, 和田 卓人 |本 | 通販 | Amazon
施策デザインのための機械学習入門〜データ分析技術のビジネス活用における正しい考え方 | 齋藤 優太, 安井 翔太, 株式会社ホクソエム |本 | 通販 | Amazon
Pythonではじめる数理最適化: ケーススタディでモデリングのスキルを身につけよう | 岩永二郎, 石原響太, 西村直樹, 田中一樹 |本 | 通販 | Amazon
来年の話
1月~3月
週1×3が確定で、現時点で未定ですが月1の仕事も継続になる見込みです。
稼働率的にはかなりいい感じなのですが、
2021年は年初に始めた仕事の他には新しい取組みを一切しなかったので
週1ぐらいの薄い仕事があれば手を出してみたいかなと考えています。
法人化
昨年末時点で法人化については
「自分がやる意義も見いだせないし
中小企業が増える社会的な意義もない」と感じていました。
これについては1年経った今でも変わりませんが
税金があまりにも高いので
綺麗ごとも言ってられず形だけ法人化することにしました。
諸々準備して2022年の秋頃を予定しています。
スキル・知識面の振り返り
分析実務系
今年はStanで込み入ったモデルを作ったり
特許を出願できるようなアルゴリズムを書いたりすることは少なく、
データを正しく集計・可視化するためのデータベースの整備や
バイアスを緩和するロジックの設計などに専ら取り組みました。
諸々の環境が整ってきたこともあり、機械学習アルゴリズムを用いたり、
学習済みモデルを用いて予測したりなど上辺の「データサイエンス」は
エンジニアが容易に代替できる状況になってきました。
一方、上辺の「データサイエンス」にも必要な
データの管理や整備については汎用化が難しい泥臭い作業が必要で
適切にできる&やりたい人材が圧倒的に不足しているのが現状と認識しています。
私としてもあまり好きでも得意でもない領域ですが
ここに労力をかけるのが最もROIが高いと思われる場面が多いので
来年以降も携わることになるかなと感じています。
そういえば、今年は実務で初めてDeep Learningを使ってみました。
Deep Learningと言っても浅いAuto Encoderなのですが
情報を一次元に埋め込んで
sin,cosの層を挟み二次元に復元して円周上に配置するという
アイデアが上手くハマって面白いな~と思ったりしました。
ビジネス系
今年はエンジニア組織に付随するような形のポジションの仕事ばかりだったので
事業や組織の管理などに関わることはなく、書籍などのインプットもしませんでした。
積極的に関与するとストレスフルな場面が多いので
関わらなくて上手く回ってくれるならばそれに越したことはないですね。
収入面の振り返り
週5以上で働いていた期間が長くなり、昨年の約1.3倍になりました。
来年は法人化して収入を抑えるので
もう二度とこんな額にはならないでしょう。さよならふるさと納税の日々。
来年もどうぞ宜しくお願い致します。
独立後2年目の振り返りなど
今年はコロナで世界が大きく変わってしまった1年でした。
独立して2年目の記録を残しておきます。
今年の仕事
1月~5月
年明けから週2×2 + 週1×1 という感じで3社の仕事を行っていたのですが、
参加していたプロジェクトの1つがコロナ直撃により解散することになりました。
プロジェクトのフェーズとしてあまりにも道半ばだったので、
外的要因でこんな形で終わることもあるのかあという気持ちになりました。
6月~7月
週2×1 + 週1×1という低負荷の状態になり、のんびり積読を消化していました。
以下はこの期間に限らず、今年読んで良かったなと思ったものです。
名著と呼ばれているものはやはり名著なんだなと思いました。
ファスト&スロー あなたの意思はどのように決まるか? 文庫 (上)(下)セット | |本 | 通販 | Amazon
企業変革の実務 いつ、何を、どの順番で行えば現場は動くか | 小森 哲郎 |本 | 通販 | Amazon
Kaggleで勝つデータ分析の技術 | 門脇 大輔, 阪田 隆司, 保坂 桂佑, 平松 雄司 |本 | 通販 | Amazon
8月~12月
新たに案件を紹介いただき、週2×2 + 週1×1というフル稼働に戻りました。
新しい案件では事業会社のマーケティング部門の方と一緒に、
ウェブからのデータ収集や整備、ダッシュボードの設計などを行っています。
データサイエンティストとしてのスキルを使うことは少ないのですが
これまでやったことないの役割でかつ、
一緒に取り組んでいる方々にも喜んでもらえているので満足しています。
また、9月には以前一緒に働いたことのあるコンサルの方からお声がけいただき、
DX案件の提案に協力しました。結果としては失注したのですが、
コンサルの働き方を体感できたのは良かったです。
私にはコンサルのクレイジーな働き方は真似できないので
「コンサルはするけどコンサルじゃない」というポジションで
この先もいきたいなと思いました。
そして、独立直後から続けていた週2の仕事は
腰を据えて長期的な視点で色々取組んでいたのですが、
コロナの影響でそんな呑気なことを言ってられない状況になってしまいました。
私自身の仕事の幅も制限され、会社側に取っても私の費用対効果が低いので
契約は更新しないつもりだったのですが、なんやかんやで
1月以降も月1日程度の薄い契約を残すことになりました。
月1稼働でその分の価値が出せるのか現段階では全く想像できないのですが
成り立つ様に頑張りたいと思います。
来年の話
1月~2月
週2で継続している仕事が週3に増え、
週1で継続している仕事はそのまま、
新規の仕事を週2で、上記の薄い仕事を月1で行うことになります(125%稼働)。
もうあまり若くないので、正直こんなに頑張りたくないのですが、
一緒に働いたことがある人を増やすことは投資と考えて
いただいた話はなるべく断らない様にしています。
(当然、単価やポリシーの問題で即お断りするものもあります。)
それでも現状、リソースの問題で断らざるを得ない話もあり
申し訳なく感じるとともに、ビジネス的にも機会損失だなと感じています。
法人化?
そこで、法人化して人を増やせたら解消するかと考えてみると、
今の市況を考えるとおそらく上手く解消すると思うんですよね。
週3稼働の人を年500万円ぐらいで1,2人雇用しても経営的に無理はなさそうです。
人が増えれば、案件の数も増やせるので稼働率も安定して
さらに人を増やせて… という道筋もぼんやり見えます。
ただ、既に数えきれないほど分析系の会社がある中で
自分が同種のビジネスをやる意味がどれほどあるのだろうかという点が
引っ掛かります。
ビッグデータブームの前であれば、ブレインパッドの様に分析に特化した集団をつくり
知見を蓄積して世の中にサービスを提供する意味は大きかったでしょう。
また、ちゅらデータの様に地方を拠点とすることで
労働問題を改善するという狙いも素晴らしいものだと思います。
そんな中、2020年代に、東京で、私がやる意味を考えると、なかなか難しいです。
労働者側にとって都合が良い会社はやる意味が少しはあるかなと思いますが、
まだスイッチが入る感じではないです。
また別の観点として、似たビジネスを行う規模の小さい会社が乱立するのは
労働生産性の観点から社会全体的には微妙なことなんじゃないかとも考えています。
現状は国が小さい会社を守る姿勢を取っていたりする(税金面など)ので
それほど気にすべきことではないのかもしれませんが。
長期的に世の中がどうなるのが理想的であって
その中で自分がどういうポジションを取っていくべきなのかは
もう少しじっくり考えてみようと思います。
スキル・知識面
分析実務系
これまでほとんど手をつけていなかった
KerasやPytorchなどディープラーニング系のフレームワークを触ってみました。
感触はある程度掴めたと思いますが
「めちゃくちゃ面白い!」という領域までは到達できなかったので
必要になるまでしばらく放置する感じだと思います。
その他、エンジニア的な立ち回りをする機会が増えてきたので
WEB周り(CSS, JavaScript)やdockerなども積極的に触る様になった1年でした。
ビジネス系
上で挙げた「企業変革の実務」を読んだぐらいでしたが、
企業の普遍的な問題構造や、根本治療をしていく道筋が描かれていて
これはとても勉強になりました。成熟した事業を行っている会社で
経営に携わっている人にはおすすめしたいなと思いました。
収入面
年間を通してほぼ週5で働いていたこともあり、昨年の約1.6倍になりました。
第一感は「やったー」ですが、これを目指したかった訳じゃないんだよなと。
来年も3月までは忙しいですが、それ以降はゆっくり考える時間を確保したいです。
来年もどうぞ宜しくお願い致します。
お金回りの話
個人事業主として今年経験したり調べたりしたことをメモしておきます。
記載内容は2020年時点のものであるので
今後変更される可能性があることにご注意ください。
国民年金、付加保険料、国民年金基金、個人型確定拠出年金(iDeCo)
フルタイムの会社員から個人事業主になると、
国民年金の制度において第二号被保険者から第一号被保険者という区分に変わります。
この区分は厚生年金に加入しているかどうかで決まります。
各区分に関する年金制度については、以下の図が分かりやすいです。
(本来、この様な図を国が提供するべきだと思うのですが、
民間企業が提供しているものしか見つけられませんでした。)
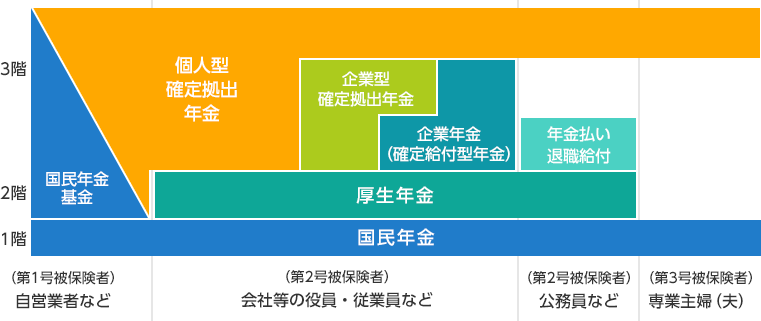
日本の年金制度 | 年金の基礎知識 | 企業型確定拠出年金 | 野村の確定拠出年金ねっと
基本的に第二号被保険者は
確定拠出年金の運用方法を考えるぐらいしかありませんが
第一号被保険者になると以下のような自由度が出てきます。
・国民年金基金と個人型確定拠出年金の配分(合わせて6.8万円/月)を決める
・国民年金基金に加入しない場合に国民年金付加保険料を払うかどうか決める
国民年金基金と個人型確定拠出年金
これらの違いをざっくり説明すると
国民年金基金は加入時にプランを決めて年金額を確定させるのに対して
個人型確定拠出年金は運用成績により年金額が変動する点が1番大きいと思います。
つまり単純化すると、リスクを抑制したければ前者の比重を
リターンを追求したければ後者の比重を上げるのが良いという感じです。
私としてはリターンを追求したいわけではなかったので
国民年金基金の割合を大きくするつもりで資料請求などもしたのですが
あることに気付いてしまいました。
基金が解散した場合の取り扱いについて
基金は公的な制度として、国民年金法に基づきその設立から運営について厚生労働省から指導、監督を受け、代議員会での議決を経て運営されております。また基金の財政状況を毎年チェックし、健全な運営に努めております。基金の財政状況は決算書に記載されていますので、随時閲覧できます。仮に当基金が解散した場合は国民年金法に基づき、基金の解散時点での残余財産額を加入員および受給者等で分配することとなっており、それまで支払われた掛金額を下回ることがあります。なお、分配される額を国民年金基金連合会へ移管して、将来年金として受け取ることができるような措置を講じております。
重要なお知らせ | 手続きの流れを見る | 国民年金基金連合会
そして、事業概況を確認すると
加入者は平成15年度の約80万人をピークに減少を続け
令和元年には約35万人となっています。
私が60歳になる頃、何人残っているのでしょうか。
https://www.npfa.or.jp/state/R1genzon.pdf
また、財政状況を確認すると
増加し続ける責任準備金に対して純資産が不足している状況が
データが閲覧できる平成22年以降ずっと続いています。
現在加入している方の年齢構成が分からないので、
もしかしたら10年後ぐらいに解消するのかもしれませんが
よくわかりません。
https://www.npfa.or.jp/state/R1nenkinzaisei.pdf
以上から、私が年金を貰い始める前に解散するリスクが高い気がして
当面は加入しないことにしました。
この先もしかしたら財政状況が改善するかもしれないですし
残りの運用期間が短くなれば個人型確定拠出年金の割合を減らすかもしれないので
その時にまた検討することにします。
国民健康保険、健康保険(任意継続)
国民年金と国民健康保険の加入をセットで行う人が多いと思いますが
会社員として加入していた健康保険組合の任意継続制度を利用して
最大2年間健康保険に加入し続けることもできます。
健康保険を続ける場合、会社員のときとは違って事業主負担がなくなるため
それほどメリットがない場合も多いのですが、
退職時の給与が低かった場合や給与以外の所得が多かった場合などは
任意継続することで保険料を安くできる可能性が高いです。
小規模企業共済、経営セーフティ共済
国が中小企業政策としてやっているものですが
個人事業主も利用できる代表的な節税策です。
前者は掛け金(最大84万円/年)が全額所得控除となり、
後者は掛け金(最大240万円/年、通算で800万円まで)が経費にできます。
どちらもある程度の期間続けていれば
掛け金を取り戻せる仕組みになっています。
中身を理解して、即入りたいと思ったわけですが
小規模企業共済については「加入資格のない例」として
「アパート経営等の事業を兼業している給与所得者
(法人または個人事業主と常時雇用関係にある方)(※)」というのがありました。
※の部分には給与所得があっても加入できる例外が記載されていましたが
判断基準がよく分かりませんでした。
全体の所得に占める割合は少ないものの
私は契約社員の給与所得もあったので、電話で問い合わせてみました。
なぜか歯切れよく回答してくれませんでしたが結論としては以下の様でした。
・加入する時点で固定の給与所得があるとNG。
日給だけが決まっている様な契約であればOK。
・一旦、加入した後に固定の給与所得が発生するようになっても
それを理由に解約する必要はない。
私はしばらく固定の給与を貰い続けるので
経営セーフティ共済にだけ入ることにしました。
持続化給付金、家賃支援給付金(国、東京都)
これらは来年以降はなさそうなので、簡単に記載します。
持続化給付金は個人事業主は最大100万円貰えるという大変嬉しい制度でした。
青色申告の場合は給付の条件もゆるく、手続きも簡単でした。
一方、国の家賃支援給付金は
私が自宅を事業所としていることもあって貰える額が小さかったのですが
書類の審査が無駄に厳しく、スピードも遅くストレスが溜まりました。
持続化給付金でOKだった文書を出しているのに、
「売上台帳」の文言がないとか、全部同じ色だと該当の月が分からないという理由で
差し戻され、事務局の運用コストも相当無駄だなと感じました。
また、国の家賃支援給付金の申請が終わらないと
東京都の申請ができない仕組みになっていたので余計にイライラした気がします。
東京都の家賃支援給付金は手続きも簡単で、振り込みも早かったです。素晴らしい。
個人事業税
秋頃に、都の主税局から「個人の事業内容に関するお尋ね」なる
何も悪いことはしていないのにドキっとする書類が届きました。
内容は事業内容を把握して課税するかどうかを決めるというものでした。
どうせ払わなければいけないものだろうと思って素直に
データサイエンティストとして
顧客のデータ活用に関する取り組みに対する助言および
簡易的なプログラムを開発している旨を記載して返送しました。
それから数週間後に
「あなたの業種の判断を決めかねている」という電話が掛かってきました。
課税するためには何らかの法定業種というものに当てはめる必要がある様で、
「コンサルタント」だと該当するが「プログラマー」だと該当しないとのことでした。
個人事業税 | 税金の種類 | 東京都主税局
プログラムを書いている時間の方が長いのか短いのか、
プログラミングを行わない場合もあるのか、
プログラムは納品物なのかなど色々お話をした結果、
「コンサルティングだけを切り出して業務を行っているわけではないので
該当しない」との判断をいただき、非課税ということになりました。
書類が届いた時点で払う気満々になっていたので、とても得した気分になりました。
ただ、本来的には法定業種が今の世の中に追従できていないだけな気がするので
アップデートされて課税されるのが正しい気がしています。
この他、個人として個人年金保険やNISAについても調べて
今年から適用を受けていますが、
個人事業主に限った話ではないので省きます(書く余力なし)。
また最近はエンジェル税制というのも気になっています。
これについては改めて書くかもしれません。
Maximal Information Coefficientの使い方
たまには技術系の話も書いてみます。
水準数が少ない変数に対して
Maximal Information Coefficient(MIC)を計算する場合は注意が必要という話です。
MICはだいぶ昔に話を聞いて便利そうだなーと思っていたのですが
これまで実際に使う機会はありませんでした。
www.slideshare.net
使う機会がなかった理由は
基本的に私は初期の段階からモデルを意識してアプローチすることが多く、
「データマイニング」的な機械的な関係性抽出をあまり行わないからだと思います。
また、もしそういうことを行う場合は
機械学習のモデルを作って特徴量重要度を見ることが多かったです。
今回はたまたま「機械学習」というワードを使わず
「相関係数」の一種ということで話を済ませた方が良さそうな状況だったので
Rの{minerva}を使ってみることにしました。
使う前の私の認識は以下でした。
・出力される値は0~1となり、完全な関連がある場合は1となる。
・連続変数でも離散変数でも離散化することになるので気にせず使える。
しかし実際に使ってみると、離散変数の場合は完全に一致していても
出力が1にならない場合があることに気付きました。
> library(minerva) > > set.seed(1) > x1 <- rpois(10000,1) > table(x1,x1) x1 x1 0 1 2 3 4 5 6 7 0 3700 0 0 0 0 0 0 0 1 0 3599 0 0 0 0 0 0 2 0 0 1862 0 0 0 0 0 3 0 0 0 653 0 0 0 0 4 0 0 0 0 161 0 0 0 5 0 0 0 0 0 22 0 0 6 0 0 0 0 0 0 2 0 7 0 0 0 0 0 0 0 1 > mine(x=x1,y=x1)$MIC [1] 0.9914476
当然ですが、19,20世紀に開発された
Pearson, Spearman, Kendallの相関係数は1となります。
> cor(x1,x1,method="pearson") [1] 1 > cor(x1,x1,method="spearman") [1] 1 > cor(x1,x1,method="kendall") [1] 1
また、上記のケースではMICでも1に近い値となっていましたが
下記の様に0に近い値になることもあります。これは困ります。
> set.seed(1) > x2 <- rpois(10000,0.01) > table(x2,x2) x2 x2 0 1 0 9904 0 1 0 96 > mine(x=x2,y=x2)$MIC [1] 0.07812958
当初、アルゴリズムのパラメータの設定が原因なのではないかと思ったのですが
それは本質的ではありませんでした。
このようなことが起こるのは、MICで計算している相互情報量の性質に依るからです。
MICのアルゴリズムを簡単に説明すると
2つの変数に対して様々な離散化を行って相互情報量を計算した上で
最大の相互情報量を出力するというものです。
(正確には出力が1を超えないようにするため
離散化した水準数での補正がかかります。)
直感的な理解として
相互情報量は2つの変数間で共有する情報量を表しているため
情報量の少ない方の変数の情報量が相互情報量の上限となります。
加えて、離散化した変数の情報量は水準間で全く偏りがないときに最大となり
1つの水準に全てが集中しているときに最小(=0)となります。
つまり、離散化した変数がどちらかでも偏っている場合は
相互情報量は小さい値になってしまいます。
連続変数の様に水準数が多い変数であれば
偏りの少ない離散化を行える可能性が高くなるため問題はありませんが、
上記で見たような水準数の少ない変数については
離散化のバリエーションが少なくなるため
強い関連があってもMICが大きくならない場合があるということです。
長々と書いてきましたが、これを改善するのは簡単で
水準間の差よりも小さなノイズを加えて水準数を増やしてあげれば良いです。
> set.seed(1) > noise <- runif(10000,min=-0.1,max=0.1) > mine(x=x2+noise,y=x2+noise)$MIC [1] 1
ノイズを加えたことでMICが大きく下がることはない気がしていますが、未検証です。
悪影響が小さいのであれば、アルゴリズム側で吸収してくれると嬉しいですね。
MICの詳しい計算手続きについては以下の資料が分かりやすかったです。
http://lectures.molgen.mpg.de/algsysbio12/MINEPresentation.pdf
この資料はこちらで知りました。ありがとうございます。
誤解等あれば教えていただけると幸いです。